Fully homomorphic encryption 全同态加密
同态加密
同态加密是一种加密形式,它允许在不先解密的情况下对其加密数据执行计算,且计算结果任然保持加密。这非常的有用,比如说你想通过 DNA 找寻你的亲人,但你又想对自己的 DNA 数据保密,这时同态加密就起作用啦,你可以上传加密后的 DNA 数据到数据库,然后他们就可以为你提供匹配服务并将结果返还给你。而在这过程中,服务提供者对这些数据是完全不知情的。
常见的类型有:部分同态 (partially homomorphic) 、有点同态 (somewhat homomorphic) 、分级完全同态 (leveled fully homomorphic) 和完全同态 (fully homomorphic) 加密。
- 部分同态仅支持一种类型的同态操作,如加法、乘法,因此通常最为高效,可以对密文执行无限次的加法或乘法运算
- 有点同态同时支持加法和乘法的同态操作,因此它比部分同态更通用,不过只能执行有限次数的同态操作
- 分级完全同态与有点同态类似,都是受限的电路系列,但二者的区别在于使用 LFHE 可以提前“计划”要计算哪种类型的函数(即达到什么深度)
- 完全同态则允许对加密消息进行大量不同类型的评估操作,次数不受限制,是同态加密的最强概念。
总的来说就是,部分同态可以无限制的加或者乘,全同态是无限制的加和乘,有点同态 (somewhat) 是有限制的加和乘。
最初在20世纪70年代提出,但直到 2009 年才可用,所以这是一个相当新的领域
当今最有效的方案有:TFHE、BGV, BFV、CKKS 等
通常同态加密有五个步骤:
-
设置
选择加密的方案、一些安全参数和一些功能的性能参数
-
密钥生成
包括私钥 (Secret key) 、公钥 (public key) 、重线性化密钥 (relinearization key) 和伽罗华密钥 (Galois keys) ,其中后三者是公开的
-
加密
在这里我们加密数字向量
-
评估
-
解密
SIMD 计算
A single instruction multiple data,单指令多数据。
当你发出单个指令时,它对所有数据进行操作,我们将同态加密与SIMD一起使用。
消息是向量,然后将消息编码为明文,明文是多项式,密文是加密后的输出,且密文将具有随机的外观。即,你无法区分你是在加密一条消息还是多条消息,因为密文总是看起来是随机的。
消息类的数量与多项式的次数有关,次数越高,消息槽越多,并行性也就越高。
多项式环
一个系数为整数的多项式
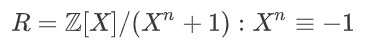
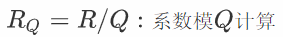
注意这里的 Q 是零平衡的,例如:Q = 5 时,系数的取值范围为 {-2, -1, 0, 1, 2} ,而不是 0~4
接下来的所有计算都遵循上面的规则
最重要的参数是 n 和 log(Q) ,这两个参数决定了安全性
编码和加密
编码器会将消息向量映射到多项式,也就是明文
加密器会将明文多项式变成密文,实际上就是通过增加噪点来掩盖明文
然后每次加密都是随机化的密文,所以即使加密相同的明文也总是会生成不同的密文,以此确保其安全性
噪点
有一个安全区,它会将信息与噪点分开,解密时可以用密钥将噪点移除,但随着每一次的同态计算噪点会越来越大,当噪点增加到破坏了其安全区时,解密就会失败。乘法引入的噪点最大。
解密和解码
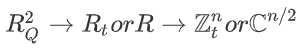
Subscribe to bbbiggest's blog
Get the latest posts delivered right to your inbox